mnorm()
Description:
Normalize a matrix or a multidimensional matrix, during which the center value is 0 and the standard deviation is 1.
Syntax:
mnorm(A, n)
Note:
An external library function (See External Library Guide) where parameter n is the sequence number of the level on which the summarization is performed. If n is absent, the desired dimension is the first one whose size is not 1 in matrix A.
Parameter:
|
A |
A matrix or a multidimensional matrix. |
|
n |
A positive integer. |
Option:
|
@s |
Handle the normalization using a statistical method where n-1 is the divisor. |
Return value:
Sequence
Example:
|
|
A |
|
||||
|
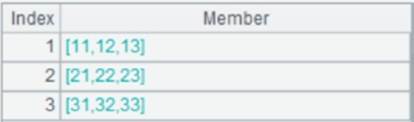
1 |
[[11,12,13],[21,22,23],[31,32,33]] |
|
||||
|
2 |
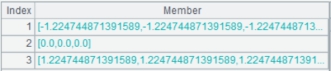
=mnorm(A1,1) |
Normalize matrix A1’s first level, that is, normalization by column. |
||||
|
3 |
=mnorm(A1, 2) |
Normalize matrix A1’s second level, that is, normalization by row. |
||||
|
4 |
=mnorm(A1) |
Normalize matrix A1’s first level since parameter n is absent. |
||||
|
6 |
=mnorm@s(A1) |
Normalization using the statistical method. |
||||
|
7 |
[[[111,112,113],[121,122,123],[131,132,133]],[[211,212,213],[221,222,223],[231,232,233]]] |
Define a three-dimension matrix whose two members are 3*3 matrices. |
||||
|
8 |
=mnorm(A6, 1) |
Normalize matrix A6’s first level, that is, normalization on the two member matrices in alignment. |
||||
|
9 |
=mnorm(A6, 2) |
Normalize matrix A6’s second level, that is, normalization each of the two member matrices by column. |